Công thức lượng giác cơ bản
Lượng giác là một nhánh của toán học nghiên cứu mối quan hệ giữa các góc và các giá trị lượng giác của các cạnh của một tam giác. Các giá trị lượng giác của một góc là các hàm số của góc đó, và có thể được dùng để tính toán các cạnh và góc của tam giác.
Lượng giác có nhiều ứng dụng trong thực tế, bao gồm:
- Đo đạc: Lượng giác được sử dụng để đo đạc khoảng cách, góc và diện tích.
- Thiên văn học: Lượng giác được sử dụng để xác định vị trí của các thiên thể.
- Kỹ thuật: Lượng giác được sử dụng trong thiết kế và xây dựng.
- Vật lý: Lượng giác được sử dụng trong cơ học, quang học và điện từ học.
Khái niệm, vai trò của các công thức lượng giác
Các công thức lượng giác là các công thức quan trọng trong lượng giác, được sử dụng để tính toán các giá trị lượng giác của các góc. Các công thức lượng giác bao gồm:
- Công thức lượng giác của sin, cos, tan, cot, sec, csc trong tam giác vuông
- Công thức lượng giác cộng, trừ
- Công thức lượng giác nhân, chia
- Công thức lượng giác biến đổi
Vai trò của các công thức lượng giác cơ bản
Các công thức lượng giác có vai trò quan trọng trong lượng giác, cụ thể như sau:
- Giúp tính toán các giá trị lượng giác của các góc: Các công thức lượng giác là công cụ quan trọng để tính toán các giá trị lượng giác của các góc.
- Giúp giải các bài toán lượng giác: Các công thức lượng giác được sử dụng để giải các bài toán lượng giác, bao gồm các bài toán về tam giác, về hàm lượng giác và về các ứng dụng của lượng giác.
- Giúp hiểu rõ bản chất của lượng giác: Các công thức lượng giác giúp người học hiểu rõ bản chất của lượng giác, từ đó có thể ứng dụng lượng giác một cách hiệu quả.
Tầm quan trọng của việc nắm vững các công thức lượng giác
Việc nắm vững các công thức lượng giác là rất quan trọng đối với người học lượng giác. Các công thức lượng giác cơ bản là nền tảng để học các kiến thức lượng giác nâng cao. Đồng thời, các công thức lượng giác cũng được sử dụng trong nhiều lĩnh vực của thực tế, vì vậy việc nắm vững các công thức này sẽ giúp người học có thể ứng dụng lượng giác một cách hiệu quả.Tham khảo: Phân có tác dụng cải tạo đất

Bảng công thức lượng giácTrong tam giác vuông, các giá trị lượng giác của một góc được xác định như sau:
- Sin: Tỉ số giữa cạnh đối diện với góc so với cạnh huyền.
- Cos: Tỉ số giữa cạnh kề với góc so với cạnh huyền.
- Tan: Tỉ số giữa cạnh đối diện với góc so với cạnh kề với góc.
- Cot: Tỉ số giữa cạnh kề với góc so với cạnh đối diện với góc.
- Sec: Tỉ số giữa cạnh huyền so với cạnh kề với góc.
- Csc: Tỉ số giữa cạnh huyền so với cạnh đối diện với góc.
Công thức lượng giác
Dưới đây là một số công thức lượng giác biến đổi thường gặp:
Công thức sin của 2 góc:
sin(2α) = 2sinαcosα
Công thức cos của 2 góc:
cos(2α) = cos^2α - sin^2α = 1 - 2sin^2α
Công thức tan của 2 góc:
tan(2α) = 2tanα / (1 - tan^2α)
Công thức cot của 2 góc:
cot(2α) = 1 / tan(2α) = (1 - tan^2α) / 2tanα
Công thức sec của 2 góc:
sec(2α) = 1 / cos(2α) = 1 / (cos^2α - sin^2α)
Công thức csc của 2 góc:
csc(2α) = 1 / sin(2α) = (1 - sin^2α) / 2sinα
Trên đây là một số công thức lượng giác cơ bản và biến đổi thường gặp. Việc nắm vững các công thức này là rất quan trọng đối với người học lượng giác.

Bảng công thức lượng giácCác công thức lượng giác cộng, trừ được sử dụng để tính toán giá trị lượng giác của tổng hoặc hiệu của hai góc.
Công thức lượng giác cộng
- sin(α + β) = sinαcosβ + cosαsinβ
- cos(α + β) = cosαcosβ - sinαsinβ
- tan(α + β) = (tanα + tanβ) / (1 - tanαtanβ)
Công thức lượng giác trừ
- sin(α - β) = sinαcosβ - cosαsinβ
- cos(α - β) = cosαcosβ + sinαsinβ
- tan(α - β) = (tanα - tanβ) / (1 + tanαtanβ)
Ví dụ
Tính giá trị của sin(30° + 60°)
sin(30° + 60°) = sin30°cos60° + cos30°sin60°
= 1/2 * 1/2 + √3/2 * √3/2
= 1/4 + 3/4
= 1
Lưu ý
Các công thức lượng giác cộng, trừ chỉ áp dụng cho các góc có cùng đơn vị đo.
Các công thức lượng giác cộng, trừ có thể được suy ra từ định lý cos của tam giác vuông.
Cách học thuộc công thức lượng giác cộng, trừ
Có nhiều cách để học thuộc công thức lượng giác cộng, trừ. Một số cách phổ biến như sau:
- Lặp lại: Lặp lại các công thức lượng giác cộng, trừ cho đến khi thuộc.
- Sử dụng phương pháp móc xích: Lập một chuỗi các công thức lượng giác cộng, trừ, sau đó sử dụng phương pháp móc xích để học thuộc.
- Sử dụng sơ đồ tư duy: Vẽ sơ đồ tư duy để thể hiện mối quan hệ giữa các công thức lượng giác cộng, trừ.
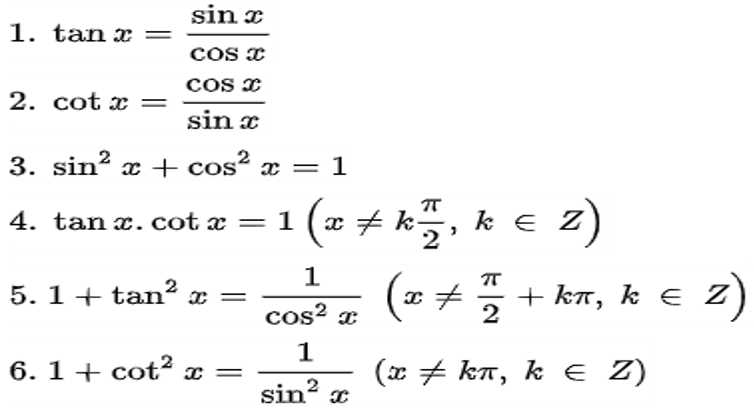
Bảng công thức lượng giácCông thức lượng giác biến đổi là các công thức được suy ra từ các công thức lượng giác cơ bản. Các công thức lượng giác biến đổi có thể được sử dụng để tính toán các giá trị lượng giác của các góc khác nhau.
Dưới đây là một số công thức lượng giác biến đổi thường gặp:
Công thức sin của 3 góc:
sin(3α) = 3sinα - 4sin^3α
Công thức cos của 3 góc:
cos(3α) = 4cos^3α - 3cosα
Công thức tan của 3 góc:
tan(3α) = (3tanα - tan^3α) / (1 - 3tan^2α)
Công thức cot của 3 góc:
cot(3α) = (1 - 3tan^2α) / (3tanα - tan^3α)
Công thức sec của 3 góc:
sec(3α) = 1 / cos(3α) = (4cos^3α - 3cosα) / (cos^2α - 3sin^2α)
Công thức csc của 3 góc:
csc(3α) = 1 / sin(3α) = (1 - sin^2α) / (3sinα - 4sin^3α)