Công thức lượng giác cơ bản
Lượng giác là một nhánh của toán học nghiên cứu về các mối quan hệ giữa các cạnh và góc của các tam giác. Lượng giác có ứng dụng rộng rãi trong nhiều lĩnh vực khác nhau, bao gồm:
- Toán học
- Vật lý
- Kỹ thuật
- Thiên văn học
- Đo đạc
Lịch sử của lượng giác
Lượng giác có nguồn gốc từ Hy Lạp cổ đại, khi các nhà toán học bắt đầu nghiên cứu các mối quan hệ giữa các cạnh và góc của các tam giác để giải các bài toán về đo đạc.
Các nhà toán học Hy Lạp cổ đại đã phát triển một số định lý lượng giác cơ bản, bao gồm định lý Pytago và định lý Sine.
Vào thế kỷ 17, các nhà toán học châu u đã phát triển thêm các công thức lượng giác phức tạp hơn, bao gồm các công thức về tích phân và Lượng giác
Tham khảo: Trực tiếp đá gà Campuchia
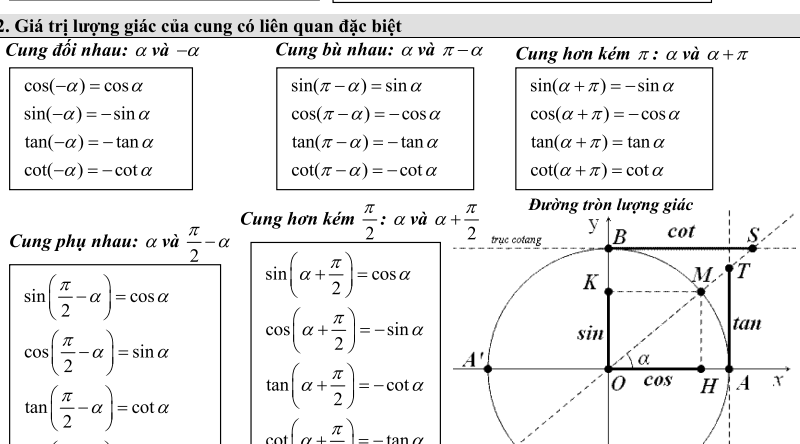
Lượng giácLượng giác có nhiều công thức, được sử dụng để tính toán các giá trị của các hàm lượng giác. Một số công thức lượng giác cơ bản bao gồm:
- Công thức sin, cos, tan của một góc
- Công thức lượng giác của tổng và hiệu của hai góc
- Công thức lượng giác của một góc gấp đôi và một góc ba lần
- Công thức lượng giác của một góc nửa và một góc một phần tư
Sine (sin)
Hàm sin của một góc trong một tam giác vuông là tỉ số giữa cạnh đối diện với góc đó và cạnh huyền.
Cosin (cos)
Hàm cos của một góc trong một tam giác vuông là tỉ số giữa cạnh kề với góc đó và cạnh huyền.
Tangent (tan)
Hàm tan của một góc trong một tam giác vuông là tỉ số giữa cạnh đối diện với góc đó và cạnh kề với góc đó.
Cotangent (cot)
Hàm cot của một góc trong một tam giác vuông là tỉ số nghịch của hàm tan, là tỉ số giữa cạnh kề với góc đó và cạnh đối diện với góc đó.
Secant (sec)
Hàm sec của một góc trong một tam giác vuông là tỉ số giữa cạnh huyền và cạnh kề với góc đó.
Cosecant (csc)
Hàm csc của một góc trong một tam giác vuông là tỉ số nghịch của hàm sec, là tỉ số giữa cạnh huyền và cạnh đối diện với góc đó.
Ví dụ
Cho tam giác vuông ABC với góc A là góc cần tính hàm lượng giác.
- Sine: sin A = BC/AC
- Cosin: cos A = AB/AC
- Tangent: tan A = BC/AB
- Cotangent: cot A = AB/BC
- Secant: sec A = AC/AB
- Cosecant: csc A = AC/BC
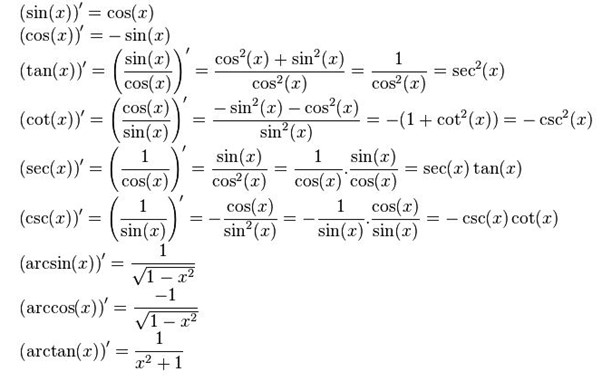
Lượng giácCó nhiều công thức lượng giác, được sử dụng để tính toán các giá trị của các hàm lượng giác. Một số công thức lượng giác cơ bản bao gồm:
Công thức sin, cos, tan của một góc
- sin A = √(1 - cos^2 A)
- cos A = √(1 - sin^2 A)
- tan A = sin A / cos A
Công thức lượng giác của tổng và hiệu của hai góc
- sin (A+B) = sin A*cos B + cos A*sin B
- sin (A-B) = sin A*cos B - cos A*sin B
- cos (A+B) = cos A*cos B - sin A*sin B
- cos (A-B) = cos A*cos B + sin A*sin B
- tan (A+B) = (tan A+tan B) / (1-tan A*tan B)
- tan (A - B) = (tan A-tan B) / (1+tan A*tan B)
Công thức lượng giác của một góc gấp đôi và một góc ba lần
- sin 2A = 2 sin A cos A
- cos 2A = cos^2 A - sin^2 A = 2 cos^2 A - 1 = 1 - 2 sin^2 A
- tan 2A = (2 tan A) / (1 - tan^2 A)
- sin 3A = 3 sin A - 4 sin^3 A
- cos 3A = 4 cos^3 A - 3 cos A
- tan 3A = (3 tan A - tan^3 A) / (1 - 3 tan^2 A)
Công thức lượng giác của một góc nửa và một góc một phần tư
- sin A/2 = √(1 - cos A) / 2
- cos A/2 = √(1 + cos A) / 2
- tan A/2 = (1 - cos A) / (sin A)
- sin A/4 = √(2 - cos A) / 2
- cos A/4 = √(2 + cos A) / 2
- tan A/4 = (1 - cos A) / (√(2 + cos A))

Lượng giácCác hàm lượng giác có ứng dụng rộng rãi trong nhiều lĩnh vực khác nhau, bao gồm:
Toán học: Các hàm lượng giác được sử dụng trong nhiều lĩnh vực của toán học, bao gồm hình học, đại số và giải tích.
Vật lý: Các hàm lượng giác được sử dụng trong nhiều lĩnh vực của vật lý, bao gồm cơ học, điện từ học và quang học.
Kỹ thuật: Các hàm lượng giác được sử dụng trong nhiều lĩnh vực của kỹ thuật, bao gồm xây dựng, cơ khí và điện tử.
Toán học
Trong hình học, các hàm lượng giác được sử dụng để tính các cạnh và góc của các tam giác. Ví dụ, để tính chiều dài cạnh huyền của một tam giác vuông, ta có thể sử dụng công thức Pythagoras:
c^2 = a^2 + b^2
Từ đó, ta có thể tính được c bằng cách sử dụng hàm lượng giác:
c = √(a^2 + b^2)
Trong đại số, các hàm lượng giác được sử dụng để giải các phương trình và bất phương trình lượng giác. Ví dụ, để giải phương trình lượng giác sin x = 1/2, ta có thể sử dụng các công thức lượng giác để tìm các nghiệm của x.
Trong giải tích, các hàm lượng giác được sử dụng để nghiên cứu các hàm số lượng giác. Ví dụ, để nghiên cứu sự biến thiên của hàm số sin x, ta có thể sử dụng các công thức lượng giác để tìm đạo hàm và tích phân của hàm số.
Vật lý
Trong cơ học, các hàm lượng giác được sử dụng để nghiên cứu các chuyển động tròn. Ví dụ, để tính tốc độ góc của một vật chuyển động tròn, ta có thể sử dụng hàm lượng giác:
ω = v / r
Trong điện từ học, các hàm lượng giác được sử dụng để nghiên cứu các sóng điện từ. Ví dụ, để tính cường độ điện trường của một sóng điện từ, ta có thể sử dụng hàm lượng giác:
E = E_0 sin(ωt - kx)
Trong quang học, các hàm lượng giác được sử dụng để nghiên cứu các hiện tượng khúc xạ và phản xạ ánh sáng. Ví dụ, để tính góc khúc xạ của ánh sáng khi đi qua một môi trường, ta có thể sử dụng hàm lượng giác:
sin i / sin r = n_1 / n_2
Kỹ thuật
Trong xây dựng, các hàm lượng giác được sử dụng để tính toán các góc và kích thước của các công trình. Ví dụ, để tính chiều dài của một cây cột, ta có thể sử dụng hàm lượng giác để tính toán chiều cao của cây cột từ góc tạo bởi cây cột và mặt đất.
Trong cơ khí, các hàm lượng giác được sử dụng để tính toán các chuyển động của các máy móc. Ví dụ, để tính lực tác dụng lên một bánh xe, ta có thể sử dụng hàm lượng giác để tính toán mô-men xoắn tác dụng lên bánh xe.
Trong điện tử, các hàm lượng giác được sử dụng để nghiên cứu các mạch điện. Ví dụ, để tính điện áp trên một tụ điện, ta có thể sử dụng hàm lượng giác để tính toán dòng điện qua tụ điện.
Trên đây là một số thông tin về các công thức lượng giác. Hi vọng các bạn sẽ có thông tin hữu ích.