Công thức thể tích khối lập phương
Đặc điểm nổi bật
Sáu mặt vuông vắn: Mỗi mặt của khối lập phương đều là một hình vuông hoàn hảo, với bốn cạnh bằng nhau và bốn góc vuông 90 độ.
Mười hai cạnh bằng nhau: Toàn bộ mười hai cạnh của khối lập phương đều có độ dài bằng nhau, tạo nên sự cân đối và hài hòa cho hình khối.
Tám đỉnh nhọn: Tám đỉnh của khối lập phương được tạo thành bởi sự giao nhau của ba cạnh. Các đỉnh này cách đều nhau và tạo thành các góc nhọn 109,5 độ.
Đường chéo và tâm đối xứng: Bốn đường chéo của khối lập phương cắt nhau tại một điểm duy nhất, gọi là tâm đối xứng. Tâm đối xứng này cũng là giao điểm của ba đường trung tuyến trong mỗi mặt vuông.
Tính chất toán học
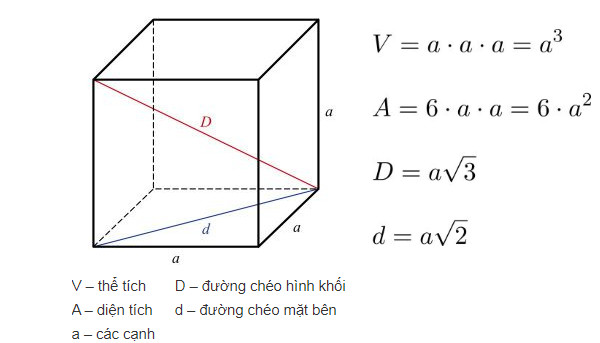
Diện tích: Diện tích toàn phần của khối lập phương bằng sáu lần diện tích một mặt, tính theo công thức 6a^2, trong đó a là độ dài cạnh.
Thể tích: Thể tích của khối lập phương bằng a^3, nghĩa là thể tích tỷ lệ lập phương với độ dài cạnh.
Đường chéo: Độ dài đường chéo của khối lập phương có thể tính bằng công thức a√3, thể hiện mối liên hệ đặc biệt giữa cạnh và đường chéo.
Ứng dụng rộng rãi
Xây dựng: Khối lập phương là đơn vị cơ bản trong xây dựng, được sử dụng để tạo nên các viên gạch, khối bê tông, và cấu trúc kiến trúc vững chãi.
Thiết kế: Hình khối lập phương được ưa chuộng trong thiết kế đồ nội thất, đồ trang trí, và các sản phẩm công nghiệp nhờ sự đơn giản, tinh tế và tính thẩm mỹ cao.
Toán học và khoa học: Khối lập phương đóng vai trò quan trọng trong nhiều lĩnh vực toán học như hình học, đại số, và giải tích. Nó cũng được ứng dụng trong vật lý, hóa học, và các ngành khoa học khác để mô phỏng cấu trúc vật chất và các hiện tượng tự nhiên.
Trò chơi và giải trí: Khối lập phương là thành phần không thể thiếu trong các trò chơi trí tuệ như Rubik, Sudoku, và trò chơi xếp hình. Nó cũng góp phần tạo nên sự thú vị và kích thích tư duy cho người chơi.
Tham khảo: Tính diện tích hình bình hành lớp 4

Khối lập phươngHình lập phương - một khối hoàn hảo với sáu mặt vuông bằng nhau, ẩn chứa trong mình những bí ẩn toán học thú vị. Nổi bật nhất chính là công thức thể tích, chìa khóa mở ra cánh cửa khám phá thế giới bên trong khối lập phương.
Công thức thể tích của khối lập phương được biểu diễn đơn giản qua ba chữ cái: V = a^3, nơi:
- V đại diện cho thể tích, thể hiện sức chứa bên trong khối lập phương.
- a chính là độ dài cạnh, là chìa khóa mở ra mọi bí ẩn.
Hãy thử tưởng tượng, nếu ta có một khối lập phương với cạnh dài a cm, ta có thể xếp đầy nó bằng a x a x a những viên xúc xắc nhỏ bé. a^3 chính là tổng thể tích của tất cả các viên xúc xắc ấy, hé lộ cho ta bí mật về sức chứa bên trong khối lập phương.
Công thức này không chỉ đơn thuần là phép tính toán, mà còn là công cụ đắc lực cho nhiều ứng dụng thực tế. Từ việc tính toán lượng nước trong bể bơi hình lập phương, đến việc xác định thể tích gỗ cần thiết để chế tạo đồ nội thất, công thức thể tích luôn sát cánh bên ta.
Hãy thử thách bản thân với những bài toán về khối lập phương, tự tay khám phá những điều kỳ diệu ẩn chứa bên trong thế giới toán học. Biết đâu, bạn sẽ là người giải mã thành công những bí ẩn tiếp theo của khối lập phương!
Thể tích khối lập phươngBạn có bao giờ bị cuốn hút bởi những khối lập phương đầy màu sắc, hoàn hảo? Hay tò mò về thể tích bên trong của chúng? Hôm nay, hành trình khám phá của chúng ta sẽ dẫn đến bí mật về cách tính thể tích khối lập phương chỉ từ diện tích mặt!
Hãy tưởng tượng một khối lập phương rực rỡ, mỗi mặt mang một diện tích riêng. Diện tích này chính là chìa khóa để mở cánh cửa dẫn đến thể tích ẩn giấu bên trong. Bí mật nằm ở đâu? Hãy cùng vén màn bí ẩn!
Công thức
Thể tích (V) của khối lập phương được tính bằng công thức đơn giản sau:
V = (Diện tích mặt) ^ (3/2)
Giải thích
Diện tích mặt: Đây là diện tích của một mặt bất kỳ của khối lập phương.
^ (3/2): Ký hiệu lũy thừa, nghĩa là "bình phương của diện tích mặt, sau đó nhân với căn bậc ba của kết quả".
Ví dụ
Giả sử bạn có một khối lập phương với diện tích mỗi mặt là 4 cm². Áp dụng công thức, ta có:
V = (4 cm²) ^ (3/2) = (16 cm²) ^ (1/2) ≈ 8 cm³
Bằng cách sử dụng công thức đơn giản này, bạn có thể dễ dàng xác định thể tích của khối lập phương chỉ từ diện tích mặt. Khám phá này mở ra cánh cửa cho vô số ứng dụng thú vị trong toán học, khoa học và kỹ thuật.
Thể tích khối lập phươngHãy tưởng tượng một khối hộp chữ nhật với chiều dài, chiều rộng và chiều cao được ký hiệu lần lượt là l, r và h. Thể tích của khối hộp chữ nhật này được tính bằng công thức quen thuộc:
Giả sử ta có một khối lập phương với cạnh được ký hiệu là a. Thể tích của khối lập phương này được tính bằng công thức đơn giản:
- V_lập phương = a * a * a = a^3
Điều thú vị là, thể tích của khối lập phương này có mối liên hệ mật thiết với thể tích khối hộp chữ nhật ban đầu!
Bí mật được hé lộ qua công thức sau:
Hãy hình dung ta chia khối hộp chữ nhật thành 6 khối lập phương nhỏ có cạnh bằng a. Khi đó, thể tích của mỗi khối lập phương nhỏ bằng a^3. Do đó, tổng thể tích của 6 khối lập phương nhỏ này chính bằng thể tích của khối hộp chữ nhật ban đầu, hay:
- 6 * a^3 = V_hộp
Suy ra:
Công thức này mang lại cho bạn sức mạnh giải mã thể tích khối lập phương từ những thông tin về khối hộp chữ nhật:
- Bước 1: Tính thể tích khối hộp chữ nhật bằng công thức V_hộp = l * r * h.
- Bước 2: Áp dụng công thức bí mật V_lập phương = V_hộp / 6 để tìm thể tích khối lập phương.
Trên đây là các công thức thể tích khối lập phương từ dễ đến khó. Hi vọng các bạn đã có cho mình thông tin hữu ích.