Tính diện tích hình bình hành lớp 4
Hình bình hành ẩn chứa nhiều điều thú vị hơn bạn tưởng tượng! Hãy cùng bước vào hành trình khám phá đặc điểm, tính chất và ứng dụng đa dạng của tứ giác đặc biệt này.
Định nghĩa
Hình bình hành là một dạng hình tứ giác có hai cặp cạnh đối song song với nhau. Nói cách khác, tưởng tượng hai đường thẳng song song được "nối" bởi bốn điểm, ta sẽ thu được hình bình hành.
Dấu hiệu nhận biết
Có hai cặp cạnh đối song song.
Có hai cặp cạnh đối bằng nhau.
Tứ giác có hai đường chéo cắt giao nhau tại trung điểm của mỗi đường.
Có hai góc đối bằng nhau.
Tính chất
Các cạnh đối song song và bằng nhau.
Các góc đối bằng nhau.
Đường chéo chia đôi mỗi góc mà nó đi qua thành hai góc bằng nhau.
Tổng hai góc kề một cạnh bằng 180 độ.
Diện tích hình bình hành bằng tích độ dài hai cạnh kề nhân với sin góc xen giữa chúng.
Phân loại
Hình chữ nhật: Có tất cả các góc vuông.
Hình thoi: Là hình bình hành có tất cả các cạnh bằng nhau.

Hình bình hànhHình bình hành - tưởng chừng đơn giản chỉ là tứ giác với các cặp cạnh đối song song và bằng nhau - lại ẩn chứa vô số điều thú vị và ứng dụng bất ngờ trong cuộc sống. Hãy cùng dấn thân vào hành trình khám phá thế giới hình bình hành, vượt ra khỏi phạm vi giáo khoa và khơi dậy niềm đam mê tìm hiểu toán học!
Định nghĩa và Tính chất
Hình bình hành: Tứ giác có các cặp cạnh đối song song và bằng nhau.
Tính chất:
Các góc đối bằng nhau.
Hình bình hành có các Đường chéo giao nhau tại trung điểm của riêng mỗi đường.
Diện tích: S = a * h (a: cạnh đáy, h: chiều cao)
Chu vi: C = 2(a + b) (a, b: cạnh)
Dấu hiệu nhận biết: Có 4 dấu hiệu để xác định hình bình hành.
Ứng dụng rộng lớn
Kiến trúc: Cửa sổ, cửa ra vào, vách ngăn,... hình bình hành mang đến sự thanh lịch, tinh tế, đồng thời tối ưu hóa không gian.
Kỹ thuật: Cấu trúc khung xe, bánh răng, lò xo,... hình bình hành đảm bảo độ bền bỉ, chịu lực tốt và chuyển động trơn tru.
Nghệ thuật: Thảm họa tiết, tranh vẽ, hoa văn,... hình bình hành tạo sự cân bằng thị giác, thu hút và truyền tải thông điệp nghệ thuật.
Thời trang: Khăn quàng cổ, họa tiết trang phục,... hình bình hành mang đến nét độc đáo, cá tính và phong cách riêng.
Vật dụng hàng ngày: Cánh cửa tủ, nắp hộp, khay đựng,... hình bình hành tối ưu hóa diện tích sử dụng và tăng tính thẩm mỹ.
Hình bình hànhChào mừng bạn đến với thế giới kỳ thú của hình bình hành! Hôm nay, chúng ta sẽ cùng nhau khám phá cách tính diện tích hình bình hành lớp 4 nhé!
Hình bình hành là gì?
Hãy tưởng tượng một tứ giác có các cặp cạnh đối diện song song với nhau. Đó chính là hình bình hành! Bật mí thêm cho bạn, các góc đối diện của hình bình hành cũng bằng nhau và hai đường chéo của nó cắt nhau tại trung điểm của mỗi đường.
Công thức tính diện tích hình bình hành lớp 4
Bí mật diện tích hình bình hành nằm ở công thức sau:
Diện tích = Cạnh đáy x Chiều cao
Hãy nhớ kỹ công thức này, nó sẽ là chìa khóa giúp bạn giải mã mọi bài toán về diện tích hình bình hành đấy!
Ví dụ
Giả sử bạn có một hình bình hành với độ dài cạnh đáy là 5cm và chiều cao là 4cm. Vậy diện tích của hình bình hành đó sẽ là:
Diện tích = 5cm x 4cm = 20cm²
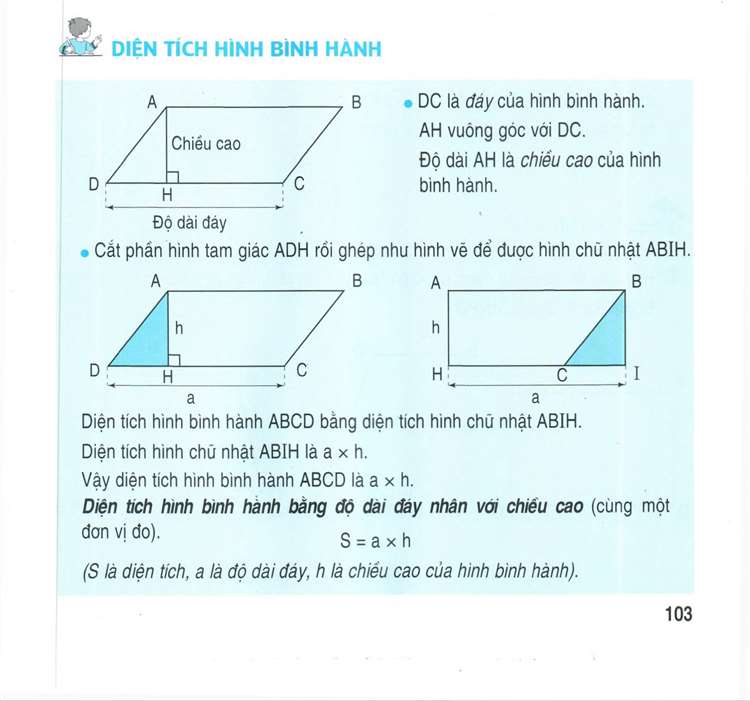
Công thức diện tích hình bình hànhBài 1
Hình bình hành ABCD có AB = 5 cm và BC = 6 cm. Tính diện tích hình bình hành ABCD.
Giải:
Áp dụng công thức tính diện tích hình bình hành:
S = a x h
Với a là độ dài đáy và h là chiều cao.
Ta có:
a = BC = 6 cm
h = AB = 5 cm
Vậy diện tích hình bình hành ABCD là:
S = 6 x 5 = 30 cm^2
Đáp án: Diện tích hình bình hành ABCD là 30 cm^2.
Bài 2
Hình bình hành ABCD có AB = 8 cm và AC = 10 cm. Tính diện tích hình bình hành ABCD.
Giải:
Ta có:
a = AB/2 = 8/2 = 4 cm
h = AC = 10 cm
Diện tích hình bình hành ABCD là:
S = a x h = 4 x 10 = 40 cm^2
Đáp án: Diện tích hình bình hành ABCD là 40 cm^2.
Bài 3
Hình bình hành ABCD có góc A = 45 độ và AB = 6 cm. Tính diện tích hình bình hành ABCD.
Giải:
Chiều cao của hình bình hành bằng cạnh bên nhân với sin góc tạo bởi cạnh bên và đường chéo.
Ta có:
h = AB x sin(45) = 6 x √2/2 = 3√2 cm
Diện tích hình bình hành ABCD là:
S = a x h = 6 x 3√2 = 18√2 cm^2
Đáp án: Diện tích hình bình hành ABCD là 18√2 cm^2.
Bài 4
Hình bình hành ABCD có diện tích là 30 cm^2 và chiều cao là 5 cm. Tính độ dài đáy của hình bình hành.
Giải:
S = a x h
Ta có:
S = 30 cm^2
h = 5 cm
Vậy độ dài đáy của hình bình hành là:
a = S/h = 30/5 = 6 cm
Đáp án: Độ dài đáy của hình bình hành là 6 cm.
Bài 5:
Hình bình hành ABCD có độ dài đáy là 8 cm và diện tích là 40 cm^2. Tính chiều cao của hình bình hành.
Giải:
Áp dụng công thức tính diện tích hình bình hành:
S = a x h
Ta có:
a = 8 cm
S = 40 cm^2
Vậy chiều cao của hình bình hành là:
h = S/a = 40/8 = 5 cm
Đáp án: Chiều cao của hình bình hành là 5 cm.
Các bài tập trên chỉ là ví dụ minh họa. Học sinh có thể tự luyện tập thêm nhiều bài tập khác để nâng cao khả năng tính diện tích hình bình hành.
Khi giải các bài tập, học sinh cần chú ý đến các công thức tính diện tích hình bình hành và cách áp dụng công thức vào từng trường hợp cụ thể.
Có thể sử dụng các hình vẽ minh họa để giúp giải bài tập dễ dàng hơn.
Trên đây là các tính diện tích hình bình hành lớp 4 và các bài tập cơ bản. Hi vọng các bạn sẽ có cho mình thông tin hữu ích.